原料分切下料问题及求解算法的 C# 实现

当前位置：点晴教程→知识管理交流 →『技术文档交流』

admin

2025年8月23日 23:39 本文热度 21

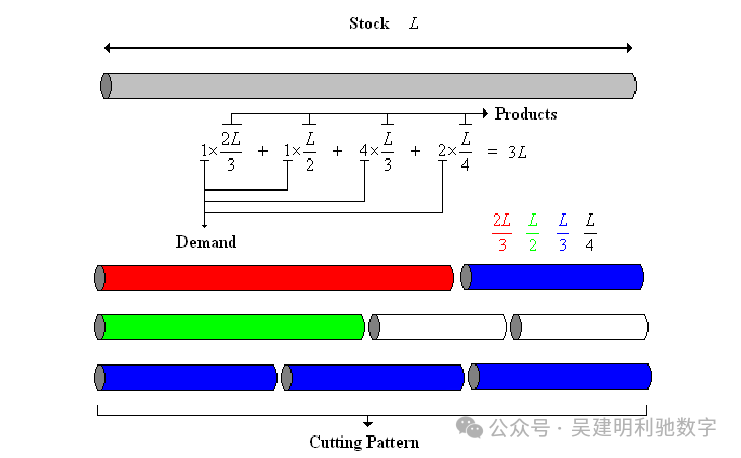
在制造业和材料加工中，常常需要将固定长度的原材料切割成不同长度以满足客户订单。

例如，一根长度为 1500mm 的金属棒，需要切成 200mm、500mm 和 700mm 的若干段，如何切割才能满足需求并尽量减少浪费？

这就是经典的 下料问题（Cutting Stock Problem）。

本文将深入介绍下料问题的数学建模、两种主流启发式算法（FFD、BFD），并提供一个 C# 测试文件驱动实现方案，方便在实际生产中直接应用。

一、问题定义与数学模型

问题描述

• 已知：

• 原材料长度
• 切割宽度（刀具损耗或端锯切宽）
• 需求列表，表示长度为的零件需要数量

• 目标：
换句话说，我们希望最小化剩余长度之和：
其中为使用的原材料数量，为第根原材料的切割长度集合。

• 为每根原材料设计切割方案，使得所有需求都得到满足，并最小化浪费。

数学模型（整数线性规划）

设二进制变量：

约束条件：

1、每个零件必须放置：

2、每根原料长度不超过限制：

目标函数：

该问题属于 NP-hard，因此对于大规模数据，启发式算法通常比精确求解更实用。

二、主流启发式算法

1. FFD（First-Fit Decreasing）

算法步骤：

1. 将需求按长度从大到小排序。
2. 按顺序尝试放入已有的原料：

• 如果当前原料剩余长度足够，则放入。
• 否则，新开一根原料。

3. 重复直到所有零件都分配完成。

复杂度分析：

排序：，放置操作最坏情况，总复杂度。

2. BFD（Best-Fit Decreasing）

算法步骤：

1. 将需求按长度从大到小排序。
2. 每次放置零件时，选择剩余长度最小但足够容纳的原料。
3. 如果找不到合适原料，则新开一根原料。

复杂度分析：

同样为，通常比 FFD 更节省原料浪费。

三、测试驱动实现

数据模型

public class JobItem
{
    public string Name { get; set; }
    public int Length { get; set; }
    public int Quantity { get; set; }
}

public class Job
{
    public int MaxLength { get; set; }
    public int CutWidth { get; set; }
    public List<JobItem> TargetSizes { get; set; }
}

public class Stock
{
    public List<JobItem> Cuts { get; set; } = new List<JobItem>();
    public int MaxLength { get; set; }
    public int CutWidth { get; set; }
    public int UsedLength => Cuts.Sum(c => c.Length) + (Cuts.Count - 1) * CutWidth;
    public int RemainingLength => MaxLength - UsedLength;
}

FFD 算法实现

public static List<Stock> SolveFFD(Job job)
{
    var sizes = job.TargetSizes
                   .SelectMany(s => Enumerable.Repeat(s, s.Quantity))
                   .OrderByDescending(s => s.Length)
                   .ToList();

    List<Stock> stocks = new List<Stock>();
    
    foreach (var item in sizes)
    {
        bool placed = false;
        foreach (var stock in stocks)
        {
            if (stock.RemainingLength >= item.Length)
            {
                stock.Cuts.Add(item);
                placed = true;
                break;
            }
        }
        if (!placed)
        {
            stocks.Add(new Stock
            {
                MaxLength = job.MaxLength,
                CutWidth = job.CutWidth,
                Cuts = new List<JobItem> { item }
            });
        }
    }
    return stocks;
}

BFD 算法实现

public static List<Stock> SolveBFD(Job job)
{
    var sizes = job.TargetSizes
                   .SelectMany(s => Enumerable.Repeat(s, s.Quantity))
                   .OrderByDescending(s => s.Length)
                   .ToList();

    List<Stock> stocks = new List<Stock>();

    foreach (var item in sizes)
    {
        Stock bestStock = null;
        int minRem = int.MaxValue;

        foreach (var stock in stocks)
        {
            if (stock.RemainingLength >= item.Length && stock.RemainingLength - item.Length < minRem)
            {
                minRem = stock.RemainingLength - item.Length;
                bestStock = stock;
            }
        }

        if (bestStock != null)
        {
            bestStock.Cuts.Add(item);
        }
        else
        {
            stocks.Add(new Stock
            {
                MaxLength = job.MaxLength,
                CutWidth = job.CutWidth,
                Cuts = new List<JobItem> { item }
            });
        }
    }
    return stocks;
}

文件驱动主程序

using System.Text.Json;

class Program
{
    static void Main()
    {
        string inputPath = "job.json";
        string outputFFD = "output_ffd.json";
        string outputBFD = "output_bfd.json";

        Job job = JsonSerializer.Deserialize<Job>(File.ReadAllText(inputPath));

        var ffdStocks = SolveFFD(job);
        var bfdStocks = SolveBFD(job);

        File.WriteAllText(outputFFD, JsonSerializer.Serialize(ffdStocks, new JsonSerializerOptions { WriteIndented = true }));
        File.WriteAllText(outputBFD, JsonSerializer.Serialize(bfdStocks, new JsonSerializerOptions { WriteIndented = true }));

        Console.WriteLine("FFD 和 BFD 求解完成，输出已生成。");
    }
}

输入示例 (`job.json`)

{
  "MaxLength":1500,
  "CutWidth":50,
  "TargetSizes":[
    {"Name":"片段1","Length":200,"Quantity":8},
    {"Name":"片段2","Length":500,"Quantity":4},
    {"Name":"片段3","Length":700,"Quantity":2}
    ]
}